OpenCL Fast Fourier Transform

Higher radix kernels

Radix-4 kernel

We will now merge two consecutive iterations. Two iterations of the FFT radix-2 algorithm will combine 4 sub-sequences of length p into one sequence of length 4p, corresponding to a "radix-4" algorithm.

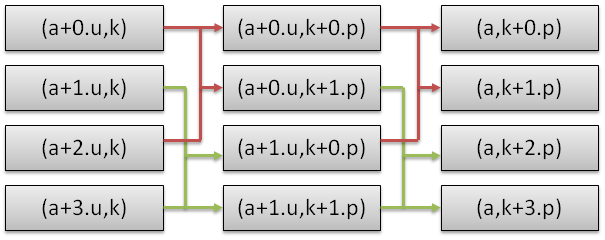
The radix-4 butterfly simplifies to a length 4 DFT applied on scaled inputs (a+0.u,k)_p, (a+1.u,k)_p * ω¹, (a+2.u,k)_p * ω², and (a+3.u,k)_p * ω³, where ω=e^-2*π*i/(2p).

First, we have to define the following new functions and macros:

// twiddle_P_Q(A) returns A * EXP(-P*PI*i/Q)
real2_t twiddle_1_2(real2_t a)
{
  // A * (-i)
  return (real2_t)(a.y,-a.x);
}

// In-place DFT-4, output is (a,c,b,d). Arguments must be variables.
#define DFT4(a,b,c,d) { DFT2(a,c); DFT2(b,d); d=twiddle_1_2(d); DFT2(a,b); DFT2(c,d); }

The radix-4 forward kernel is:

// Compute T x DFT-4.
// T is the number of threads.
// N = 4*T is the size of input vectors.
// X[N], Y[N]
// P is the length of input sub-sequences: 1,4,16,...,T.
// Each DFT-4 has input (X[I],X[I+T],X[I+2*T],X[I+3*T]), I=0..T-1,
// and output (Y[J],Y|J+P],Y[J+2*P],Y[J+3*P], J = I with two 0 bits inserted at postion P. */
__kernel void fftRadix4Kernel(__global const real2_t * x,__global real2_t * y,int p)
{
  int t = get_global_size(0); // thread count
  int i = get_global_id(0); // thread index
  int k = i&(p-1); // index in input sequence, in 0..P-1
  int j = ((i-k)<<2) + k; // output index
  real_t alpha = -FFT_PI*(real_t)k/(real_t)(2*p);

  // Read and twiddle input
  x += i;
  real2_t u0 = x[0];
  real2_t u1 = twiddle(x[t],1,alpha);
  real2_t u2 = twiddle(x[2*t],2,alpha);
  real2_t u3 = twiddle(x[3*t],3,alpha);

  // In-place DFT-4
  DFT4(u0,u1,u2,u3);

  // Shuffle and write output
  y += j;
  y[0]   = u0;
  y[p]   = u2;
  y[2*p] = u1;
  y[3*p] = u3;
}

This kernel must be called for p=1, p=4,..., p=N/4. If N is not a power of 4, one radix-2 kernel shall be inserted.