GPU Benchmarks

Available computing power

In the previous pages, all the operations we studied turned out to be limited by memory access, and we could measure the memory throughput in the CPU and the GTX285 GPU under various conditions. We will now do the same thing for the floating point operations, without memory access.

GPU computing power

Each of the T threads will compute N_ROTATIONS rotations of a V-dimensional float vector. In the GPU, the OpenCL kernel will be:

__kernel void crunch(__global float * out)
{
  vector_t x,y,cs,sn,xx,yy; // vector_t is float or float2 or float4
  x = 1.0f;
  y = 0.0f;
  cs = cos(2.0f); // random angle
  sn = sin(2.0f);
  for (int i=0;i<N_ROTATIONS;i++)
  {
    xx = cs * x - sn * y;
    yy = cs * y + sn * x;
    x = xx;
    y = yy;
  }
  out[get_global_id(0)] = dot(x,y);
}

The final dot product prevents the compiler from optimizing out unused dimensions (I'm not sure it would try, anyway...) We count 6.V floating point operations per iteration (4*mul and 2*add), and measure the number of floating point operations per second (in GFlops). N_ROTATIONS=40000 in our tests. The following values (in GFlops) are obtained for a workgroup size of 256, with a variable number of threads, from 512 to 1Mi.

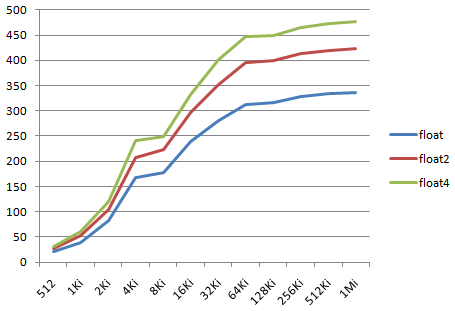
We can observe that the Flops measure growths with the number of threads, and that the dimension of the vectors has an impact on the results, from 337 (float) to 476 (float4) maximum GFlops. (beta driver 195.39 provides a 30% gain over the previous 190.89 version!) These results were obtained with the default compilation options. Using -cl-fast-relaxed-math allows us to reach 521 maximum GFlops (10% faster) for the GTX285.

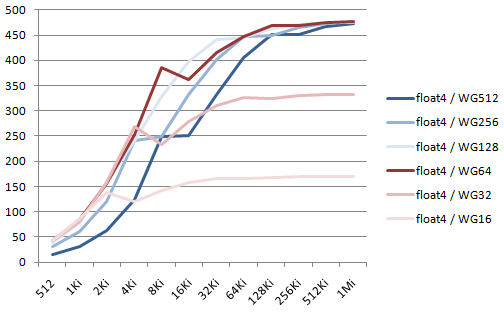
Let's measure the influence of the OpenCL workgroup size, from 16 to 512:

CPU computing power

Now let's see how fast goes the CPU on the same problem, using the corresponding SSE instructions on single float: addss, subss, mulss, and vectors of 4 float: addps, subps, and mulps. We run from 1 to 64 identical threads in parallel:

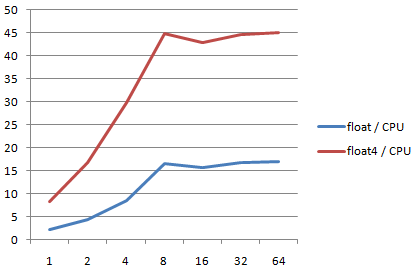
The maximum value for the Core i7 CPU is reached for at least 8 threads: even if it has 4 cores, HyperThreading allows to run more efficiently 8 threads than 4. The max value reached in our example (float4 rotations) is 45 GFlops. The performance ratio between float4 and float is approximately 3x.

So, where is the teraflop?

Giving a value to the theoretical peak computing power for the NVidia GTX 285 is apparently not so easy. The Wikipedia entry reports 1062 GFlops, as well as this well-documented page by James Hamilton: Heterogeneous Computing using GPGPUs: NVidia GT200. Some other sites report 993 GFlops.

Values effectively measured in the various benchmarks found online can reach up to 700 GFlops. To reach the highest values, the code must be optimized to use all computation units the GPU (Ports 0 and 1 on James Hamilton's page). Real world code (i.e. code computing something useful) will probably be optimizable up to 400-500 GFlops, unless limited by memory accesses.

Conclusions on computing power

• to use the full CPU computing power, at least all "advertised" threads (here 8) of the CPU must be used;
• to use the full GPU computing power, at least 32K threads and an appropriate choice of the OpenCL workgroup size must be used;
• working on float4 vectors instead of float gives a 3x gain on the CPU, and a 1.3x gain on the GPU;
• if the problem can be parallelized to thousands of identical threads, the ratio GPU/CPU can be at least 10x for pure computational power (i.e. with little or no memory access), and more like 20x if the CPU implementation is not vectorized.
• don't expect to go beyond 50% of the theoretical peak computing power of the GPU in real-world problems.

In the next page, we go back to multi precision arithmetic, with the product of a large number by a single digit.