GPU Benchmarks
Eric Bainville - Nov 2009Product by one digit
In this section we will implementation multiplication of a large number by one digit. "digits" here are numbers in 0..B-1 where B is the representation base, a power of 2.
Given a number X represented by digits xi in range -M..M, with M≥B as seen earlier. We want to multiply X it by a digit k in 0..B-1.
With GMP on the CPU, this operation is executed at 3.90 cycles per 64-bit word when data is in L1 cache. At 3.33 GHz, it corresponds to 6.83 GB/s. The execution is sequential as it requires carry propagation.
First algorithm
We can try the Avizienis approach, to compute a representation yi of the result without carry propagation:
loi = (xi * k) % B (bitwise and) hii = (xi * k) / B (bitwise shift) yi = loi + hii-1 hi-1 = 0
loi is in 0..B-1, and hii max value is (M*(B-1))/B. If we write M=q*B+r, (0≤r<B) we have M*(B-1)=(q*B+r)*(B-1)=q*B^2+(r-q)*B-r, giving for hi_i a max value of q*B+r-q-1 (r>0) or q*B-q (r=0).
Case r>0. The max value for yi is then (q+1)*B+r-q-2. This value must be ≤M, that is: (q+1)*B+r-q-2≤q*B+r, equivalent to q≥B-2. The smallest suitable value for M is then M=(B-2)*B+1. Case r=0. The max value for yi is then (q+1)*B-q-1. Having this value ≤M resolves to q≥B-1.
In conclusion, this algorithm works as soon as M≥(B-2)*B+1=(B-1)2. To have digits on 32-bit signed integers, we must take B=215 or less. Storing only 15 bits on a 32-bit word is quite inefficient.
Second algorithm
In the first approach, we expanded the product xi * k on two consecutive digits, and we have seen that in this case we had to allow digits as high as M=(B-1)2. Let's see if expanding the product on three consecutive digits allows a smaller bound.
Decompose the product |xi * k| in base B and apply the sign to the three components found: xi * k = vhii*B2 + hii*B + loi yi = loi + hii-1 + vhii-2 |hii| and |loi| are in 0..B-1 hi-1 = vhi-1 = vhi-2 = 0
Here, after a derivation similar to the previous one, we obtain the condition M≥2*B-1, which is much more efficient (at least for storage) than the first algorithm. On 32-bit words, we can take B=230 or less.
OpenCL implementation v1
Let's try first an implementation where each thread i accesses the three input values xi, xi-1, and xi-2 and computes the product. Each value is accessed three times, and each product is computed three times. The sign is not taken into account here, to simplify the code.
__kernel void mul1_v1(int k,__global const int * x,__global int * z)
{
int i = get_global_id(0);
long z0 = ((long)k*(long)x[i]) & (long)BASE_MINUS1;
long z1 = (((long)k*(long)((i>0)?x[i-1]:0))>>LOG_BASE) & (long)BASE_MINUS1;
long z2 = (((long)k*(long)((i>1)?x[i-2]:0))>>(2*LOG_BASE)) & (long)BASE_MINUS1;
z[i] = (int)(z0+z1+z2);
}
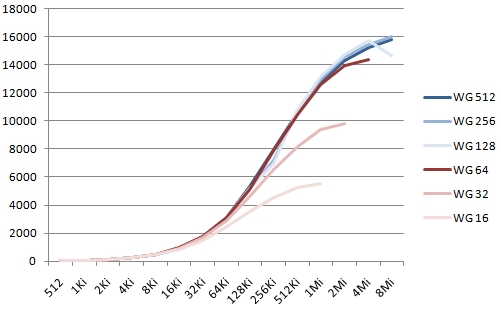
Here the running time is computed in MB of output per second. Since we use 30 bits on each 32-bit word, we count 30/8 bytes per word. On the X axis is the number of threads, corresponding to the size of the numbers, from 512 to 8Mi. Each curve corresponds to a different workgroup size, from 16 to 512 (the max value allowed by the driver). Note that the driver only accepts N/WG≤216, so a few data points are missing at the end of the curves.
For the mul1_v1 kernel, the best throughput is 16 GB/s, reached for N=8Mi and WG=256. The same kernel without the computation of z1 and z2 (i.e. with one memory read, one multiply+and, and one memory write) runs at max speed 55 GB/s (but obviously does not compute the expected result). This value is the best we can hope to reach by optimizing memory access.
OpenCL implementation v2
To optimize memory access, we will make use of OpenCL local memory: portions of the global memory buffer are copied in fast memory shared between all threads in the workgroup. In our case, we need to load WG+2 words to compute all outputs for a workgroup of size WG. The following kernel stores WG+2 products as 64-bit integers in the aux local memory.
__kernel void mul1_v2(int k,__global const int * x,__global int * z)
{
__local long aux[WORKGROUP_SIZE+2];
int i = get_global_id(0); // in X
int ii = get_local_id(0); // in workgroup
long s;
// Load X[i]*K into AUX for all threads of the workgroup + 2
s = (long)x[i];
aux[ii+2] = s * (long)k;
if (ii < 2)
{
s = (long)((i>2)?x[i-2]:0);
aux[ii] = s * (long)k;
}
barrier(CLK_LOCAL_MEM_FENCE);
// Shift, mask and sum the 3 consecutive words in each cell
s = (aux[ii]>>(2*LOG_BASE)) & (long)BASE_MINUS1;
s += (aux[ii+1]>>(LOG_BASE)) & (long)BASE_MINUS1;
s += aux[ii+2] & (long)BASE_MINUS1;
// Store the result
z[i] = (int)s;
}
The local memory syncronization (barrier) is needed because we will read values loaded by other threads in aux: thread ii initializes aux[ii+2], and then uses aux[ii], aux[ii+1], aux[ii+2].
Actually, the running time is disappointing: the best throughput we get is 18 GB/s. Time for us to run the NVidia OpenCL profiler and try to identify the issue. Here is the output of the profiler with N=220, and a workgroup size WG=256:
n 2^20 nd range size X 4096 work groups work group size X 256 work items static private mem per work group 2096 bytes registers per work item 11 registers occupancy 1.0 branch 4521 divergent branch 137 instructions 70044 warp serialize 18907 work groups per compute unit 410 gld 32b 409 gld 64b 6560 gst 64b 157868 gld request 1233 gst request 1096
The interpretation of these values given in this page has been validated by various experiments (not presented here) with simpler kernels. I could not find online resources detailing the interpretation of the output, except from the (minimal) profiler manual itself.
As stated in the profiler documentation, the reported numbers are average values for only one of the 10 "compute units". Each compute unit contains 3 "multiprocessors" (NVidia terminology), and each multiprocessor executes "warps" (NVidia terminology) of 32 parallel threads (all threads execute the same instruction).
The gst request=1096 (global store) corresponds to the number of times our kernel is executed by the compute unit, since each call writes one output z[i]. In a kernel with no branches, it seems we always have instructions=32+gst_request*n_instructions, n_instructions being the number of assembly instructions in the kernel.
In total for the 10 compute units of the GPU, we have approximately 1096*10=10960 kernel executions to compute 220 values, meaning 96 values are computed by each kernel execution inside a compute unit. It corresponds to the 3*32 threads executed by the 3 multiprocessors.
For the gld request=1233 (global load), we have the 1096 requests corresponding to the x[i] load. The remaining 137 requests are the x[-1] and x[-2] access for each workgroup.
The 2096 bytes of static private memory per work group correspond to the __local aux array (256*8 bytes), and a few more bytes. Each multiprocessor has 16KB of local memory available. Logically, all 8 warps corresponding to a workgroup should run on the same multiprocessor, and we should be limited by local memory to 7 simultaneous workgroups per multiprocessor.
OpenCL implementation v3
Enough speculating about how threads are effectively executed for now... In this version, we compute several output digits sequentially in a single thread, and see if we can raise the throughput.
__kernel void mul1_v3(int k,__global const int * x,__global int * z)
{
// Get index of block to compute
int i = get_global_id(0) * BLOCK_SIZE;
// Load the previous two values
long p0,p1,p2;
if (i>0)
{
p2 = (long)x[i-2]*(long)k; p2 >>= (2*LOG_BASE);
p1 = (long)x[i-1]*(long)k; p1 >>= LOG_BASE;
}
else p2 = p1 = 0;
// Compute the block (sequentially)
for (int j=0;j<BLOCK_SIZE;j++)
{
// Load one value
p0 = (long)x[i]*(long)k;
// Store one result computed from the last 3 values
z[i] = (int)((p0&(long)BASE_MINUS1)+(p1&(long)BASE_MINUS1)+p2);
// Shift
i++;
p2 = p1 >> LOG_BASE;
p1 = p0 >> LOG_BASE;
}
}
The first implementation mul_v1 corresponds to BLOCK_SIZE=1. The max throughput of 19.1 MB/s is reached for a workgroup size of 256 items, and BLOCK_SIZE=2.
OpenCL implementation v4
In this version, we compute and store in global memory the three components produced by each digit (with weight i, i+1, i+2), and then a second kernel reads the three components and sums them to obtain the final result. Here we have much more global memory accesses per component (4*load+4*store), but with a more regular pattern.
__kernel void mul1_v4a(int k,__global const int * x,
__global int * z0,__global int * z1,__global int * z2)
{
int i = get_global_id(0);
long u = (long)k*(long)x[i];
z0[i] = (int) (u & (long)BASE_MINUS1);
u >>= LOG_BASE;
z1[i] = (int) (u & (long)BASE_MINUS1);
u >>= LOG_BASE;
z2[i] = (int)u;
}
__kernel void mul1_v4b(__global const int * z0,__global const int * z1,__global const int * z2,
__global int * z)
{
int i = get_global_id(0);
int s = z0[i];
if (i>0) s += z1[i-1];
if (i>1) s += z2[i-2];
z[i] = s;
}
The best throughput is 10.0 MB/s reached for a workgroup size of 128. It is about half the best speed. Note that kernel mul1_v4a alone runs at 19.6 MB/s.
| GPU Benchmarks : Available Flops | Top of Page | SSE gradient |
